TensorFlow Lattice (TFL)
翻譯、整理一下TFL官方文檔
Overview
TFL是一個lattice-based model的函式庫,可以透過對模型的一些限制,將domain knowledge融合進模型中。它的優點包括適應性強、可被嚴格控制並且具有不錯的可解釋性。
Lattice
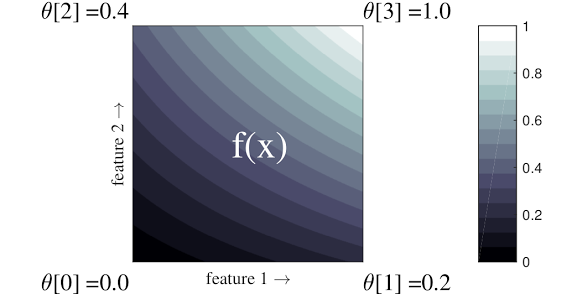
Lattice是一種透過插值來逼近輸入跟輸出關係的結構。圖中的兩個軸代表兩個輸入特徵的維度,四個頂點分別代表feature 1及feature 2為[0, 0]、[0, 1]、[1, 0]、[1, 1]時output出來的值。除了四個角落的值是模型預測出來的,其餘的整張圖都是透過這四個點之間的插值所產生。下圖的二維lattice是方便視覺化與理解才作為範本的,實際上Lattice的維度可以根據feature數量再做延伸,也可以做出其他設計。例如,增加頂點數量等等。
Calibration: 特徵校正
為了要讓feature符合lattice的條件,就必須使各個feature映射到一個最佳的區間。我個人的理解是,有些資料你覺得用線性迴歸預測出來的效果會不好,其實並不是線性回歸的問題,而是資料目前還不符合線性的條件。只要透過一個好的映射,線性迴歸的性能就能堪用在看似不能使用的資料上。例如 y=3log(x)+2 這個function明顯不是線性,但如果我讓 t=log(x) 把x映射到t後,原本的式子就會變成 y=3t+2 ,這就符合線性了。所以Calibration正是這樣一個機制,能把原始的特徵變得能夠在lattice上使用。
下圖的例子是用咖啡店離買家的距離以及價位來推算顧客滿意度的模型,我們明顯可以用常識推出距離太遠、價格太高顧客會不喜歡。另外,價格太低對要求一定品質的顧客來說反而是雷點。因此,我們透過以上的知識就能夠要求模型的映射必須滿足一些條件。由此模型可學習出下圖的piecewise linear function。最後,原本的feature就會被映射到跟output接近線性相關的區間上啦。

Common-Sense Shape Constraints
為了讓模型能夠反映出已知的知識,我們可以對模型設下一些限制來實現。
Monotonicity(單調性)
簡單來說就是要求模型必須反映出輸出對於某個特徵來說要遞增還是遞減。有時候我們可能已經知道某項特徵應該要跟輸出有明確的正或負相關,但是資料上可能因為noise或分布等問題,使得有些模型反而會將錯就錯,學習出一個太過複雜的關係。這時候我們就能用Monotonicity來加以限制。
Convexity/Concavity(凸性/凹性)
定義上就是二次微分是遞增還是遞減。這個限制搭配上Monotonicity能夠反映出邊界效應。讓某些特徵的數值在太大或太小時,他對於輸出的貢獻會逐漸趨於定值。
Unimodality(峰/谷性)
除了可以限制遞增或遞減,我們也可以要求特徵跟輸出的關係可以存在一個局部的最大或最小相關性。這就正好可以透過Unimodality控制。
Pairwise trust(特徵的可信賴程度)
有些時候,某項特徵可能在另一項特徵夠大或小的時候才能發揮影響力。例如,如果我們要預測一個運動員下一場的表現,可能會透過他過往比賽的平均數據來分析,但是若一個運動員出賽的次數過少,那麼他的比賽數據理所當然就比較沒有代表性。這時候,我們就能夠限制,當一個球員出賽的場次越多,他過往比賽的平均數據應該要有比較高的可信度。
TensorFlow Lattice (TFL)
翻譯、整理一下TFL官方文檔
Overview
TFL是一個lattice-based model的函式庫,可以透過對模型的一些限制,將domain knowledge融合進模型中。它的優點包括適應性強、可被嚴格控制並且具有不錯的可解釋性。
Lattice
Lattice是一種透過插值來逼近輸入跟輸出關係的結構。圖中的兩個軸代表兩個輸入特徵的維度,四個頂點分別代表feature 1及feature 2為[0, 0]、[0, 1]、[1, 0]、[1, 1]時output出來的值。除了四個角落的值是模型預測出來的,其餘的整張圖都是透過這四個點之間的插值所產生。下圖的二維lattice是方便視覺化與理解才作為範本的,實際上Lattice的維度可以根據feature數量再做延伸,也可以做出其他設計。例如,增加頂點數量等等。

Calibration: 特徵校正
為了要讓feature符合lattice的條件,就必須使各個feature映射到一個最佳的區間。我個人的理解是,有些資料你覺得用線性迴歸預測出來的效果會不好,其實並不是線性回歸的問題,而是資料目前還不符合線性的條件。只要透過一個好的映射,線性迴歸的性能就能堪用在看似不能使用的資料上。例如 y=3log(x)+2 這個function明顯不是線性,但如果我讓 t=log(x) 把x映射到t後,原本的式子就會變成 y=3t+2 ,這就符合線性了。所以Calibration正是這樣一個機制,能把原始的特徵變得能夠在lattice上使用。

下圖的例子是用咖啡店離買家的距離以及價位來推算顧客滿意度的模型,我們明顯可以用常識推出距離太遠、價格太高顧客會不喜歡。另外,價格太低對要求一定品質的顧客來說反而是雷點。因此,我們透過以上的知識就能夠要求模型的映射必須滿足一些條件。由此模型可學習出下圖的piecewise linear function。最後,原本的feature就會被映射到跟output接近線性相關的區間上啦。
Common-Sense Shape Constraints
為了讓模型能夠反映出已知的知識,我們可以對模型設下一些限制來實現。
Monotonicity(單調性)
簡單來說就是要求模型必須反映出輸出對於某個特徵來說要遞增還是遞減。有時候我們可能已經知道某項特徵應該要跟輸出有明確的正或負相關,但是資料上可能因為noise或分布等問題,使得有些模型反而會將錯就錯,學習出一個太過複雜的關係。這時候我們就能用Monotonicity來加以限制。
Convexity/Concavity(凸性/凹性)
定義上就是二次微分是遞增還是遞減。這個限制搭配上Monotonicity能夠反映出邊界效應。讓某些特徵的數值在太大或太小時,他對於輸出的貢獻會逐漸趨於定值。
Unimodality(峰/谷性)
除了可以限制遞增或遞減,我們也可以要求特徵跟輸出的關係可以存在一個局部的最大或最小相關性。這就正好可以透過Unimodality控制。
Pairwise trust(特徵的可信賴程度)
有些時候,某項特徵可能在另一項特徵夠大或小的時候才能發揮影響力。例如,如果我們要預測一個運動員下一場的表現,可能會透過他過往比賽的平均數據來分析,但是若一個運動員出賽的次數過少,那麼他的比賽數據理所當然就比較沒有代表性。這時候,我們就能夠限制,當一個球員出賽的場次越多,他過往比賽的平均數據應該要有比較高的可信度。