盡量白話的Diffusion Model基礎知識整理
整理給自己看的Diffusion Model基本知識
為了方便理解寫得很白話(不負責任版)
更新日期: 2024/10/22
Denoising Diffusion Probabilistic Models (DDPM)
主要源自Denoising Diffusion Probabilistic Models(2020)
一般我們可以假設人眼認為合理的影像應該會滿足某種特定的分布,用數學來表達就是一張真實圖像 \(\mathbf{x}_0\) 需要滿足 \(\mathbf{x}_0 \sim q(\mathbf{x})\) 這個分布(這邊的\(\mathbf{x}_0\)不見得一定要是圖像,你想像得出來任何適用以上假設的case都可以)。當然想也知道像圖像這類複雜的分布是很難人為的用任何已知的數學形式去表達出來的,所以有人想到是不是可以用深度學習來模擬這樣的分布,藉此幫助我們做圖像生成。如果粗淺的理解,擴散這個概念就是不管你的初始狀態 \(\mathbf{x}_0\) 長怎麼樣,反正經過長時間的擴散,各種不同的 \(\mathbf{x}_0\) 他們原始的特徵都會被稀釋掉、分布上也變得趨近一致。所以如果神經網路能逆轉這個擴散行為,用大量的擴散數據去學習反擴散的可能性,是不是就可以反過來從擴散的盡頭推測出一個合理的 \(\mathbf{x}_0\)?透過這個概念,以下的流程就被設計了出來,能夠對Diffusion為基礎的圖像生成模型進行訓練及採樣:
Forward Diffusion
在\(\mathbf{x}_0 \sim q(\mathbf{x})\)這個前提下,如果對\(\mathbf{x}_0\)添加Gaussian noise,並重複 \(T\) 次,生成出 \(\mathbf{x}_1, ..., \mathbf{x}_T\) 一系列的加噪圖像。在 \(T\) 夠大的情況下,最後生成出來的\(\mathbf{x}_T\)應該會趨近於Gaussian noise。以上操作數學上表示為:
\[\begin{aligned} q(\mathbf{x}_t|\mathbf{x}_{t-1}) &=\mathcal{N}(\mathbf{x}_t;\sqrt{1-\beta_t}\mathbf{x}_{t-1},\beta_t\mathbf{I}) \\ &=\sqrt{1-\beta_t}\mathbf{x}_{t-1}+\sqrt{\beta_t}\epsilon\qquad\epsilon\sim\mathcal{N}(0, \mathbf{I}) \end{aligned}\]
其中,每一步加噪的Gaussian noise強度由 \(\{ \beta_t \in (0, 1) \}_{t=0}^{T}\) 控制,\(\beta_t\) 會隨著 \(T\) 的上升也跟這越來越大,另外 \(\beta_t\) 也有很多種不同的schedule設計,包含linear、quadratic、cosine等等,會影響在 \(T\) 個時間步階中圖像被加噪或去噪的趨勢。
以上這個計算過程有一個好處,就是要得出 \(\mathbf{x}_t\) 時,不需要真的把中間過程的每一張圖都算出來,而是可以透過reparameterize的方式簡化(對計算過程沒興趣可以直接跳到下個紅字):
令\(\alpha_t=1-\beta_t\) 且 \(\bar{\alpha}_t=\prod_{i=1}^t \alpha_i\)
\[\begin{aligned} \mathbf{x}_t &= \sqrt{\alpha_t}\mathbf{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{\epsilon}_{t-1}\quad\text{ ;where } \boldsymbol{\epsilon}_{t-1}, \boldsymbol{\epsilon}_{t-2}, \dots \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\ &= \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \bar{\boldsymbol{\epsilon}}_{t-2} \quad\text{ ;where } \bar{\boldsymbol{\epsilon}}_{t-2} \text{ merges two Gaussians (*).} \\ &= \dots \\ &= \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon} \\ q(\mathbf{x}_t \vert \mathbf{x}_0) &= \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I}) \end{aligned}\]
這個簡化之所以可以成立是因為兩個分布的和是這樣計算的:
\[\mathcal{N}(\mathbf{0}, \sigma_1^2\mathbf{I})+\mathcal{N}(\mathbf{0}, \sigma_2^2\mathbf{I})=\mathcal{N}(\mathbf{0}, (\sigma_1^2 + \sigma_2^2)\mathbf{I})\]
這使得 \(\epsilon\) 項前面的係數(也就是標準差)能夠在推導的時候輕易的被合併。
\[\sqrt{(1 - \alpha_t) + \alpha_t (1-\alpha_{t-1})} = \sqrt{1 - \alpha_t\alpha_{t-1}}\]
這邊講了那麼多其實結論就是,我們要在給定 \(\mathbf{x}_0\) 時,求出 \(\mathbf{x}_t\) 只需要做一次以下的計算就夠了:
\[q(\mathbf{x}_t \vert \mathbf{x}_0)=\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}\tag{1}\]
其中, \(\alpha_t=1-\beta_t\text{ ; }\bar{\alpha}_t=\prod_{i=1}^t \alpha_i\)。我看到有些人之所以會誤會DDPM的訓練過程,以為訓練需要真的做數百次加噪的迭代,就是因為不清楚這個結論可以直接把迭代過程一步到位。
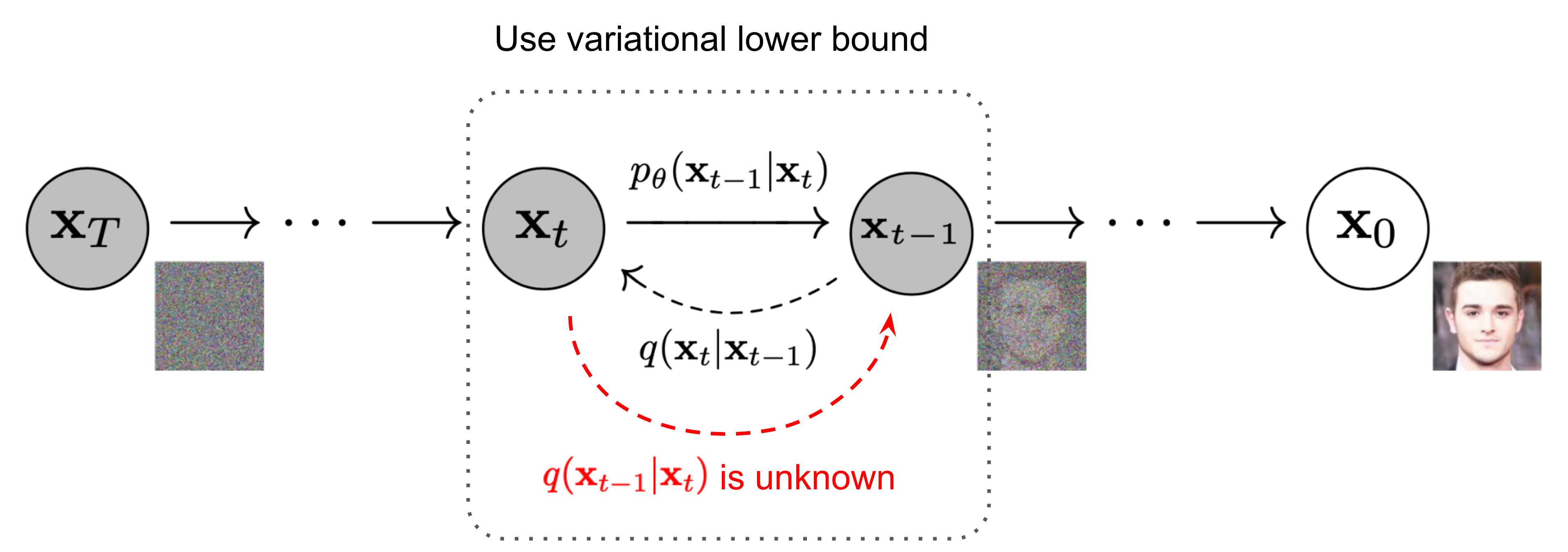
Reverse Diffusion
如果我們可以逆轉上述流程,反過來用 \(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t)\) 去推測 \(\mathbf{x}_{t-1}\),理論上就能夠從純粹的Gaussian noise \(\mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\) 中一步步還原出真實圖像 \(\mathbf{x}_0 \sim q(\mathbf{x})\)。然而,人類很難用現有的數學知識解出 \(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t)\)。但是,如果我們先假設 \(\mathbf{x}_t\) 是從 \(\mathbf{x}_0\) 一路加噪過來的,考慮 \(\mathbf{x}_0\) 這個已知的條件後,式子就能改成:
\[q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \tilde{\mu}_t(\mathbf{x}_t, \mathbf{x}_0), \tilde{\beta}_t \mathbf{I}) \tag{2}\]
而且式中的均值 \(\tilde{\mu}_t\) 和方差 \(\tilde{\beta}_t\) 可以用貝氏定理去推導出解析解(就是跟國中學的一元二次公式解差不多的意思):
\[q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = q(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0) \frac{ q(\mathbf{x}_{t-1} \vert \mathbf{x}_0) }{ q(\mathbf{x}_t \vert \mathbf{x}_0) }\]
這邊透過貝氏定理就把Reverse的條件機率改成我們已知的形式了,可以直接找Forward Diffusion中的一些結果代進去。跳過複雜的數學推導過程,總之可以得到的 \(\tilde{\mu}\) 和 \(\tilde{\beta}_t\) 解析解:
\[\begin{aligned} \tilde{\mu}_t (\mathbf{x}_t, \mathbf{x}_0) &= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \mathbf{x}_0\\ \tilde{\beta}_t &={\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \end{aligned}\]
同時把公式(1)裡的的項調換一下,就可以得到 \(\mathbf{x}_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t)\) 代入 \(\tilde{\mu}_t\) 中,得到:
\[\tilde{\mu}_t = \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)\]
解到這邊可以發現,除了 \(\epsilon_t\) 之外,其他的參數都是已知的(能透過Forward Diffusion中人為設定的 \(\beta_t\) 推算出來),最後我們就可以把求解 \(\epsilon_t\) 這個重責大任丟給神經網路處理了。所以,Reverse Diffusion的結論就是,我們要訓練一個神經網路 \(p_\theta\) 來預測 \(\epsilon_t\) ,來解出公式(2)中的分布的均值與方差,如此一來便可以採樣出 \(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t)\) 的結果了。
寫累了,有空再補充
Reference
- What
are Diffusion Models? (這篇很細,數學推導過程很完整)
- Diffusion Models:生成扩散模型 (簡中的,寫的也還行)